페이징 & 세그먼테이션
메모리 할당 방식
사용자가 사용하는 프로세스들은 메모리에 할당되게 된다.
초기 단일 사용자 시스템 (Bached Memory) - 전체 프로세스를 메모리에 통째로 할당

멀티(다중) 프로그래밍 환경에서는 process가 여러개 존재하고, context switching이 일어나게 된다.
context switching이 일어나면 → 원래 돌고있던 process가 사용하던 메모리 영역을 다음 프로세스에게 넘겨줘야 한다.
현재 실행중인 process를 disk 영역에 저장하고 → 새로운 process를 메모리에 올려줌
이 과정을 반복하게 되면 context switching overhead가 엄청나게 증가한다.
그래서 고안한 방법이
메모리를 쪼개서 할당하는 방식에는
연속 할당 방식
불연속 할당 방식
연속 할당 방식
주소 공간을 여러개로 분할하지 않고 물리적 메모리의 한 곳에 연속적으로 적재하는 방식
고정 분할 방식
물리적 메모리를 정해진 개수 만큼의 영구적인 분할로 미리 나누어 각 분할에 하나의 프로세스를 적재해 실행시키는 방식 (분할의 크기는 모두 동일하게 할 수도 있고, 서로 다르게 할 수도 있음)
하나의 분할 공간에는 하나의 프로세스만 들어간다.
동시에 메모리에 올릴 수 있는 프로그램의 수가 고정되어 있고, 프로그램의 최대 크기도 제한된다는 단점이 존재
외부 단편화, 내부 단편화 발생 가능성

단편화(Fragmentation)
외부 단편화(External Fragmentation) ✨
메모리가 할당되고 해제되는 작업이 반복되면서 작은 공간의 메모리 영역이 생기게 되는데, 이 공간이 어떤 프로세스가 필요로 하는 크기보다 작은 경우
쉽게 말해서 충분한 공간이 있지만 내가 필요로 하는 크기보다 작아서 사용할 수 없는 경우

내부 단편화 (Internal Fragmentation) ✨
프로세스에 할당된 메모리 공간이 실제로 프로세스가 필요한 공간보다 많이 할당되었을 때, 프로세스 내부에서 발생되는 단편화
아래 처럼 빈 공간 100MB가 할당되었지만, 실제로 80MB만 사용하므로 20MB가 남게 됨 → 이 공간은 너무 작아서 다른 작업들이 사용하지 못하게 되어서 내부적으로 낭비! (사용되지 않는 메모리 조각이 생기는 것)

가변(동적) 분할 방식
메모리에 적재되는 프로그램의 크기에 따라 분할의 크기, 개수가 동적으로 변하는 방식
분할의 크기를 아래처럼 프로그램의 크기에 맞게 할당하기 때문에 내부 단편화가 발생하지 않음(낭비 없음!) → 내부 단편화 해결!

그럼 만약 프로그램의 크기만큼 메모리 공간에 P1, P2, P3, P4, P5를 적재 시킨다.
그리고 P2, P4가 종료돼서 메모리에서 삭제된다면? P2, P4가 있던 공간이 비어있게 된다.
즉 아래처럼 여러곳에 메모리 가용공간(빈공간)이 생긴다.
그럼 새로운 프로그램을 어떤 가용공간에 올려야할까? →
동적 메모리 할당 문제

동적 메모리 할당 문제 (메모리 배치 기법)
최초 적합 (first-fit)
사용할 수 있는 공간(가용공간, 충분히 큰 공간) 중
가장 먼저 찾아지는 곳에 프로세스 할당어디서부터 찾는데? → 사용 가능 공간 리스트의 맨 앞에서부터 시작하거나, 이전의 최초 적합 검색이 끝났던 곳에서 다시 시작
가장 빨리 찾을 수 있기 때문에 시간적 측면에서 효율적
but 공간 활용률이 떨어진다 → 내가 필요한것 보다 훨씬 크더라도, 일단 첫번째로 발견하면 적재하기 때문

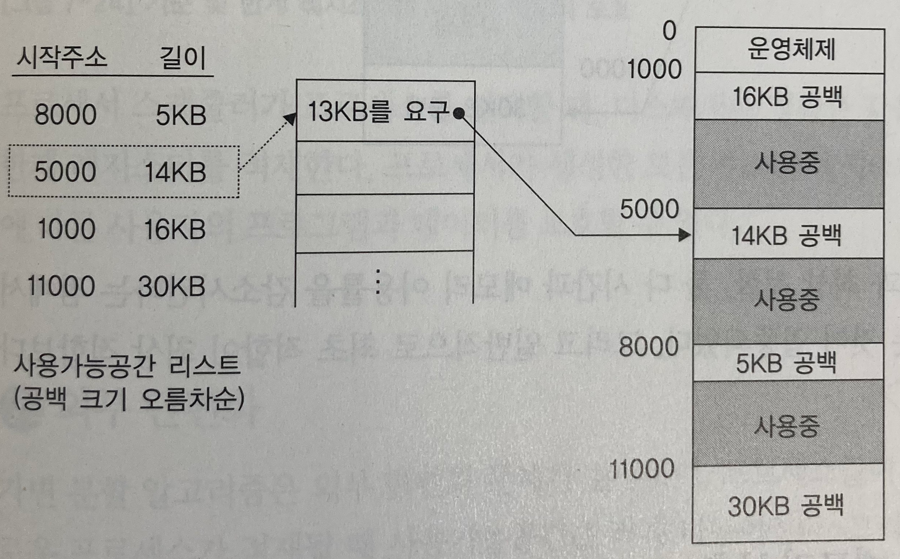
최적 적합 (best-fit)
사용 가능한
공간 리스트 중에서 가장 작은 크기의 사용 공간에 프로세스 할당최대한 딱 맞는 곳에 넣기 때문에 공간적 측면에서 효율적
but 공간 리스트가 오름차순으로 정렬되어 있지 않으면 전체 리스트를 탐색해야 함
가용 공간에 대한 지속적인 sorting 과정이 필요 (시간적 오버헤드 발생 가능성)
가장 작은 것에 맞춰 넣으려 하다보니, 매우 작은 빈 공간들을 생성해 냄
최악 적합 (worst-fit)
사용 가능한
공간 리스트 중에서 가장 큰 크기의 공간에 프로세스 할당새로운 매우 작은 가용 공간(빈 공간)들을 만들어 내지 않으므로 메모리 활용면에서 더 유용
but 최적 적합과 비슷하게 공간 리스트가 내림차순으로 정렬되어 있지 않으면 전체 리스트를 탐색해야 함 → 지속적인 sorting → 시간적 오버헤드

최초 적합 / 최상 적합 → 각각 시간과 메모리 이용률을 감소시킨다는 점에서 최악 적합보다 좋음
일반적으로 최초 적합이 최상 적합보다 메모리에 빨리 할당함!
외부 단편화 해결
메모리 통합
단편화가 발생한 빈 공간에서 인접해 있는 다른 빈 공간들을 하나로 통합시켜 큰 공간을 만드는 '통합' 방법

메모리 압축 (Memory Compaction)
가장 쉬운 방법으로는, 메모리 공간이 여러개의 조각으로 나뉘어서 빈 공간이 생기는 현상이기 때문에, 사용중인 메모리 공간을 한쪽으로 모은다면 → 충분한 공간이 생길 수 있다! 는 접근 방식
아래와 같이 흩어져 있던 빈 공간들을 하나의 연속 공간으로 만들어서(압축) 기존에 할당 할 수 없었던 프로세스를 할당!

압축의 단점,,,
이렇게 한쪽으로 모으기 위해서는 메모리 모든 내부 주소들을 재배치 해야 한다.
압축은 → 재배치가 동적인 경우에만 가능하고, run-time 시에 이루어지는 것이 특징
주소들을 동적으로 재배치 하고 → 프로세스가 이동하고 → 새로운 주소를 반영하기 위해 레지스터도 변화 → 자원의 소모가 크다!
버디 시스템 (Buddy System Algorithm)

즉, 메모리를 쪼개가면서 할당 가능한 가장 작은 블록을 찾아서 할당하는 방법
ex) 64KB 초기 블록 → 첫번째로 8KB를 요청

ex) 두번째로 8KB 요청 → 할당! (e) 처럼 할당
세번째로 4KB 요청 → (e)를 (f)로 쪼개고 (g)에 할당!
두번째로 요청한 8KB가 해제되고(h), 이어서 첫번째 요청한 8KB가 해제되면서 합쳐짐(i)

2^N 크기의 메모리를 무조건 할당해야 하기 때문에 필연적으로 내부 단편화 발생,,!!!
불연속 할당 방식
주소 공간을 불연속적으로 할당하는 방식
페이징 기법
세그먼트 기법
요구 페이징 기법
1. 페이징 기법✨
처리할 작업을 ‘동일한 크기의 페이지’로 나누어서 처리하는 것
실제 메모리를 프레임 이라고 부르는 고정 크기 블록으로 나누고, 프로세스도 페이지라고 불리는 동일한 크기의 고정된 크기 영역으로 분할한다.
→ 무슨 말이냐면,,
1000p 짜리 프로그램이 존재한다고 생각해보자
우리가 필요한 건 프로그램 1000p 전체가 아니라 400p만 필요함
그래서 프로그램을 10등분(
페이지)로 쪼개서 100p(offset) 씩 총 10묶음으로 만듦이름은 page0, page1, page2,,, 이름을 정함
그래서 실제로 필요한 page0, page1, page2, page3 4개만 메모리로 가져가게 됨 → 이걸 100p
offset을 갖는페이지라고 부른다.메모리에 실제로 올릴 때 이미 할당된 메모리 공간 아래에 자리가 남아있고, 이 자리가 4등분(
프레임)으로 분할이 되어있다. 각각의 공간은 100p의 크기에 딱 맞게 분할되어 있어서 한 프레임에 한 페이지씩 채워 넣을 수 있다. →프레임 크기 = 페이지 크기
그럼 페이지를 어떤 프레임에 넣어야할까?
위에서 page0 ,,, page3 들을 가지고 메모리 공간에 할당한다고 했는데

Page Table이라는 표를 만들어서 각각의 페이지(프로그램 조각)들을 어느 위치에 저장해 놓았는지 기록을 해놓는다.page0을 1번 프레임에,,, page3을 6번 프레임에 → 이 테이블을 보고 page0은 1번(실제 메모리 주소)에 위치하는 구나!를 알 수 있음
page table은 메모리의 어떤 공간에 쓰여진다 → page table의 시작 주소를 page table base register라는 레지스터에 저장해 놓음
그래서 실제로 어떻게 메모리 공간에 접근할까?
프로그램의 200 - 300p가 필요할 때 → 아까 분할 시킨 page2가 필요! page2 찾으러 간다.
page table에 정보를 기록해 놨으니깐 page table base register에 저장한 page table의 시작 주소를 불러와서 찾는다 → 첫 번째 메모리 참조(접근) 발생
page table의 시작주소로부터 2번째에 기록 된 내용을 본다 → page2는 3번 프레임(3번지)
페이지의 크기(offset)이 100p라는 걸 알고 있기 때문에 해당 정보를 가지고 실제 메모리의 3번지부터 시작해서 100p를 할당한다. → 두 번째 메모리 참조 발생
그래서 외부 단편화를 해결 했나?✨
네! 페이징 기법에서는 외부 단편화가 발생하지 않는다.
디스크에서 들고오는 페이지들의 크기가 프레임보다 큰 경우가 없기 때문에 메모리에 못들어가는 경우는 없다는 것 (메모리가 꽉 찬 경우는 제외)
페이징 기법을 쓰면 독립된 크기의 연속적인 공간이 없어도 프로그램을 메모리에 올려 놓을 수 있음!
그럼 내부 단편화도 해결 되나?
생각해보세요.
어떤 프로그램의 크기가 950p 이고, 200p offset을 갖는 페이지로 나눈다면, 마지막 페이지는 150p의 크기를 갖는다.
이 150p 페이지를 메모리에 넣으려면 → 200p로 나누어진 프레임에 넣는다면,,
50p만큼 내부 단편화가 생긴다.즉, 프로세스 주소 공간 중 제일 마지막에 위치한 페이지에서는 내부 단편화가 발생할 가능성이 있다!
2. 세그먼테이션
페이지, 프레임과 같이 고정 크기를 갖는 페이징과는 다른 메모리 관리 기법
프로세스를 논리적 내용을 기반으로 나눠서 메모리에 배치 → 무슨말이냐면
프로세스를
Stack
Heap
Data
Code 등으로 세그먼트로 나눌 수 있고, Code 세그먼트 안에서도
A Funtion, B Function 더 작은 세그먼트로 나눌 수 있음
이렇게 Code 영역 전체를 올리는게 아니라, A Funtion 세그먼트, B Function 세그먼트 등으로 나누어서 메모리에 올릴 수 있다는 개념
각 세그먼트들은 동일한 크기를 갖지 않는다.✨ (수행하는 기능이 다른 논리적인 집합이기 대문)
각 세그먼트들은 연속적으로 모여있어야 하지만, 메모리 안에서 세그먼트끼리 연속적일 필요는 없다.
나눈 세그먼트들을 메모리에 할당하는 방법?
페이지 할당과 비슷하게
segment table을 활용해서 메모리에 접근테이블에는 세그먼트의
번호와메모리 시작 주소,세그먼트 크기를 가짐

위 그림에서 세그먼트
0번의 위치는 어디일까?1400번지부터 크기가1000만큼 메모리에 할당된다!
메모리를 보면 각 세그먼트마다 사용하는 메모리 공간이 다 다르다
메모리에 세그먼트가 들어오고 나가고 반복하다보면, 세그먼트들 사이에 작은 빈틈들이 생길 수 있음
그 작은 빈틈보다 큰 세그먼트는 메모리에 들어올수 없는 것
외부 단편화 발생✨그럼 내부 단편화는 발생할까??? → 생각해보세요
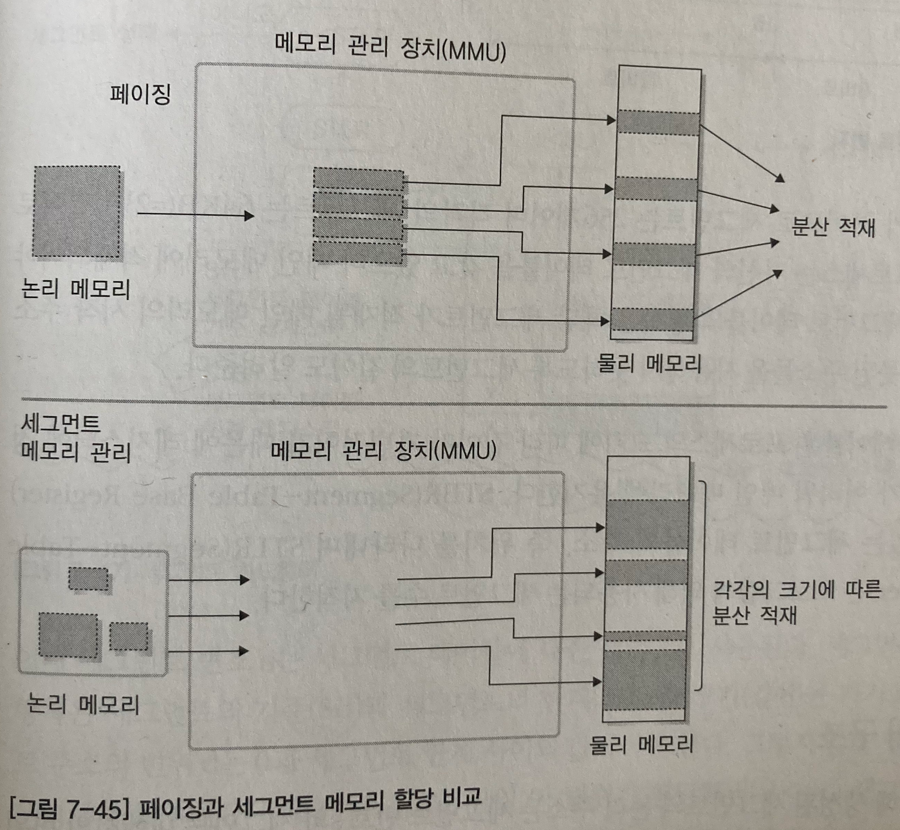
페이징 vs 세그먼테이션
페이징내부 단편화 현상을 가지고 있으나, 메모리를 효율적으로 사용할 수 있음
동일한 크기의 작업을 갖고있기 대문에 외부 단편화를 해결할 수 있고 많은 알고리즘이 개발 가능
세그먼테이션외부 단편화 현상을 가지고 있으나, 가변적인 데이터 및 모듈 크기를 가지고
세그먼트 공유와 보호의 지원이 편리함
이 두개의 장점을 적절히 섞은 것이 ‘
Paged Segmentation’ 기법 (페이지화된 세그먼트 메모리 할당 기법)페이징을 사용하기 때문에 외부 단편화를 해결할 수 있고, 세그먼테이션을 사용하기 때문에 메모리 할당 과정을 쉽게 해결

세그먼트와 페이지가 동시에 존재 → 테이블 참조해서 주소 변환을 2번 해야 하는 것 (세그먼트 테이블에서 1번, 페이지 테이블에서 1번) → 속도가 떨어진다.
변환 과정

paged segmentation 기법을 사용하면,,
페이징을 사용해서 프레임 크기 = 페이지 크기 → 외부 단편화 해결
각 세그먼트의 마지막 페이지의 크기 < 프레임 크기 → 내부 단편화 발생
내부 단편화 발생?
네
아니오
외부 단편화 발생?
아니오
네
프로시저와 데이터 분리 및 보호 여부
아니오
네
수용할 수 있는 테이블의 크기 변화가 일어나는가?
아니오
네
사용자 공유가 용이한가?
아니오
네
Last updated